श्री बालाजी प्रकाशन गणित अध्याय 1 वास्तविक संख्याएं अभ्यास प्रश्न 1.2
आज के इस लेख में हम कक्षा 10 श्री बालाजी प्रकाशन गणित अध्याय 1 वास्तविक संख्याएं का अभ्यास प्रश्न 1.2 के सवालों Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers को हल करेंगे, जिसके अंतर्गत हमारा पहला प्रश्न यह है –

Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers
अति लघुउत्तरीय प्रश्न
- यदि HCF 99, 153 = 9 तब LCM 99, 153 का मान ज्ञात कीजिए।
Ans. इस प्रश्न में आपको पहली संख्या 99 तथा दूसरी संख्या 153 दी गई है और उसका महत्तम समापवर्तक अथवा म0स0 9 दिया गया है तब हमें ल0स0 अथवा लघुत्तम समापवर्तक ज्ञात करना है। इसके लिए हमारा सूत्र है –
ल0स0 × म0स0 = पहली संख्या × दूसरी संख्या
यहां पर हमें म0स0 और पहली संख्या तथा दूसरी संख्या के मान दिए गए हैं जिसे इस सूत्र में रखेंगे।
ल0स0 × 9 = 99 × 153
अब हम ल0स0 बराबर लिखेंगे 99 * 153 / 9 और 9 से भाग कर देंगे जिससे हमारा ल0स0 का मान 1683 आ जाएगा आप नीचे यहां पर देख Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers पाओगे |

2. दो संख्याओं का म0स0 / HCF 16 तथा उनका गुणनफल 3072 है उनका ल0स0 / LCM ज्ञात कीजिए |
Ans. इस सवाल में महत्तम समापवर्तक / म0स0/ HCF 16 दिया है तथा दो संख्याओं का गुणनफल अथवा पहली संख्या तथा दूसरी संख्या का गुणनफल 3072 है तब हमें लघुत्तम समापवर्तक अथवा ल0स0 ज्ञात करना है
पहली संख्या×दूसरी संख्या = LCM×HCF
यहां पर हमें HCF और पहली संख्या तथा दूसरी संख्या के मान दिए गए हैं जिसे इस सूत्र Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers में रखेंगे।
3072 = LCM × 16
हमें एलसीएम का मान निकालना है तो हम 3072 को 16 से भाग देंगे और लिखेंगे एलसीएम बराबर 3072 / 16 और इसे भाग करने पर 192 उत्तर आ जाएगा।

3. संख्या 144 के अभाज्य गुणनखंड में 2 की घात ज्ञात कीजिए।
Ans. हमें इस सवाल में 144 संख्या दी हुई है जिसका हमें अभाज्य गुणनखंड करना है और हम अभाज्य गुणनखंड करने के बाद दो की घात कितनी बार आता है यह हमें ज्ञात Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers करना है –
अब हम अभाज्य गुणनखंड करते हैं 144 का
144= 2×2×2×2×3×3
144 का अभाज्य गुणनखंड करने पर दो दो चार बार आ रहा है और तीन तीन दो बार तो हमें इससे पता चलता है कि दो की पावर चार अर्थात 2⁴ कर होगा इससे स्पष्ट होता है कि दो की घात चार होगा |

4. संख्या 196 के अभाज्य गुणनखंडन में घातों का योग ज्ञात कीजिए।
Ans. इस प्रश्न में 196 के सबसे पहले अभाज्य गुणनखंड करने को कहा है और जिन संख्याओं की घात आएगी उन संख्याओं को उनकी घात के रूप में लिखेंगे और जो उनकी घाते होंगे उन्हें जो है हम जोड़ देंगे और हमारा उत्तर हो जाएगा।
196 =2×2×7×7
196 का गुणनखंड करने पर दो-दो 2 बार आ रहा है और सात सात दो बार आ रहा है इससे स्पष्ट होता है कि 2² की तथा 7² की घातो का योग 2 + 2 बराबर 4 होगा अर्थात इसका उत्तर 4 है ।
जिसे कुछ इस प्रकार से लगाया जाएगा आप नीचे इस सवाल का उत्तर दोबारा देख Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers सकते हैं।

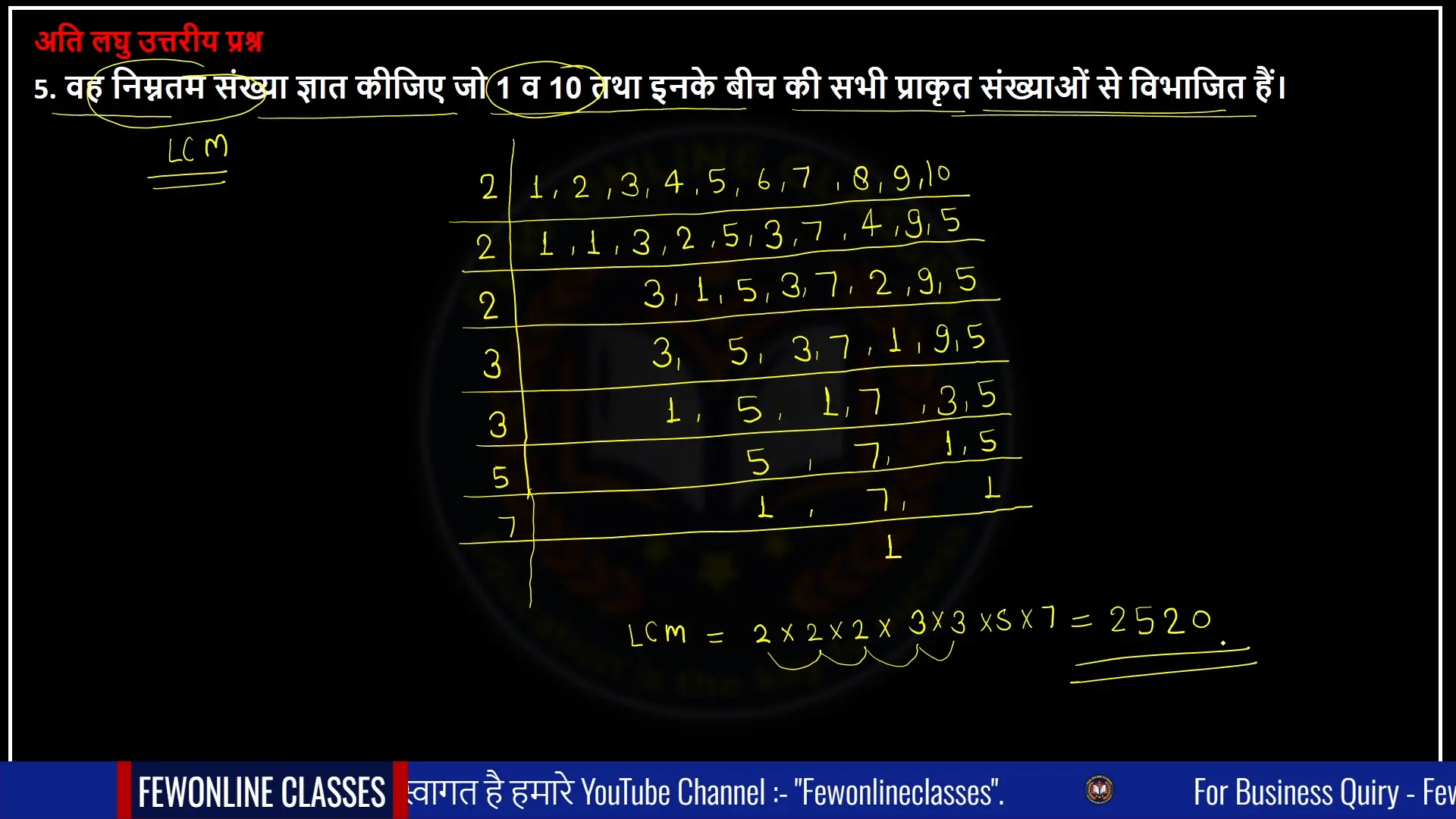
5. वह निम्नतम संख्या ज्ञात कीजिए जो 1 व 10 तथा इनके बीच की सभी प्राकृत संख्याओं से विभाजित हैं।
Ans. इस प्रश्न में दिया हुआ है कि हमें ऐसी निम्नतम संख्या का मतलब है लघुत्तम समापवर्तक ज्ञात करना है इसमें एक से 10 के बीच की सभी संख्याओं को लेना है और उनका एलसीएम निकालना है एलसीएम निकालने के बाद उनकी गुणा करवा देंगे और हमारा उत्तर हो जाएगा
1,2,3,4,5,6,7,8,9,10 का एलसीएम = 2×2×2×3×3×5×7= 2520
हम एक से 10 तक की सभी संख्याओं को कुछ इस प्रकार लिख लेते हैं और उनका एल सी एम निकालते हैं तो जो मन प्राप्त होता है उसका गुणा करने पर 2520 प्राप्त होगा जो हमारा आंसर होगा।
अगर आप इस सवाल को समझ में नहीं आ रहा है तो आप नीचे दिए गए इमेज के माध्यम से बहुत ही आसान तरीके से समझा पाओगे।
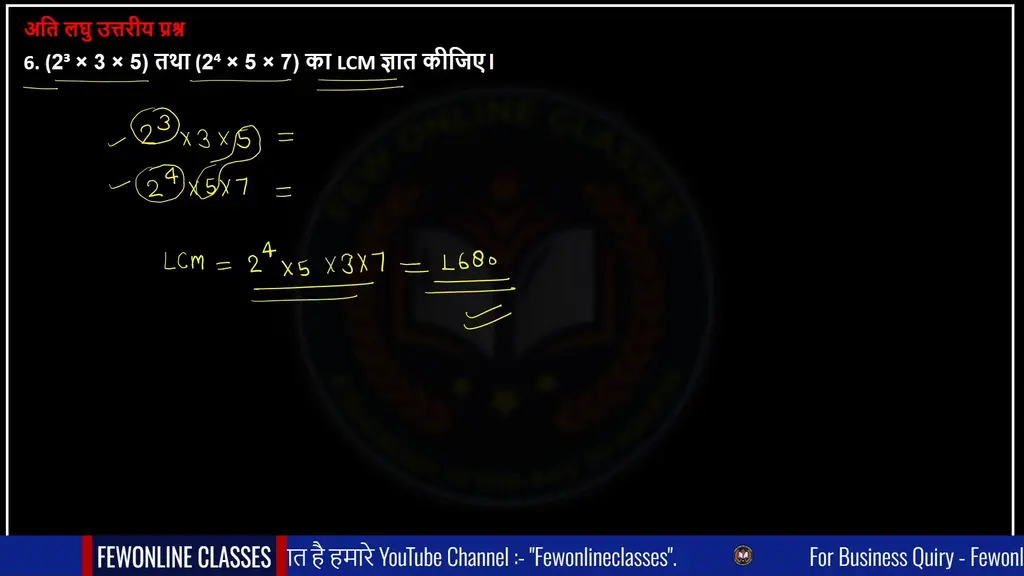
6. (2³ × 3 × 5) तथा (2⁴ × 5 × 7) का LCM ज्ञात कीजिए।
Ans. इस सवाल में आपको दो कि घात तीन * 3 * 5 तथा 2 की घात 4* 5 * 7 दिया हुआ है जिसमें हम सर्वप्रथम उसे संख्या को गुणा के रूप में लिखेंगे और फिर दोनों में से जो भी बड़ा संख्या होगी उसे नोट कर लेंगे और फिर बची हुई दोनों में से संख्याओं को नोट करके गुणा करवा देंगे तब हमारे प्रश्न का आंसर ex 1.2 class 10 math हो जाएगा।
2³ × 3 × 5 = 2×2×2×3×5
2⁴ × 5 × 7 = 2×2×2×2×5×7
Common Number = 2×2×2×5
No Common Number = 2×3×7
LCM = 2×2×2×2×3×5×7 = 1680
लघु उत्तरीय प्रश्न
7. दो संख्याओं का एचसीएफ HCF 27 तथा एलसीएम LCM 162 है यदि एक संख्या 54 है तो दूसरी संख्या ज्ञात कीजिए।
Ans. इस प्रश्न में आपको एचसीएफ 27 तथा एलसीएम 162 दिया गया है और पहली संख्या 54 है जिसमें हमें दूसरी संख्या ज्ञात करनी है
के लिए हम सर्वप्रथम फार्मूला लगाएंगे
ल0स0 × म0स0 = पहली संख्या × दूसरी संख्या
यहां पर हमें लासा मासा तथा पहली संख्या का मान दिया है जिसे हम इस सूत्र में रखेंगे
162 × 27 = 54 × दूसरी संख्या
अब हम 162 के गुण 27 से करवरकर 54 से भाग दे देंगे जिससे हमारा उत्तर 81 प्राप्त हो जाएगा जो दूसरी संख्या होगा आप नीचे दिए गए इमेज के माध्यम से देख सकते हैं और बहुत ही आसान तरीके से हल math class 10 ch 1 ex 1.2 कर सकते हैं।

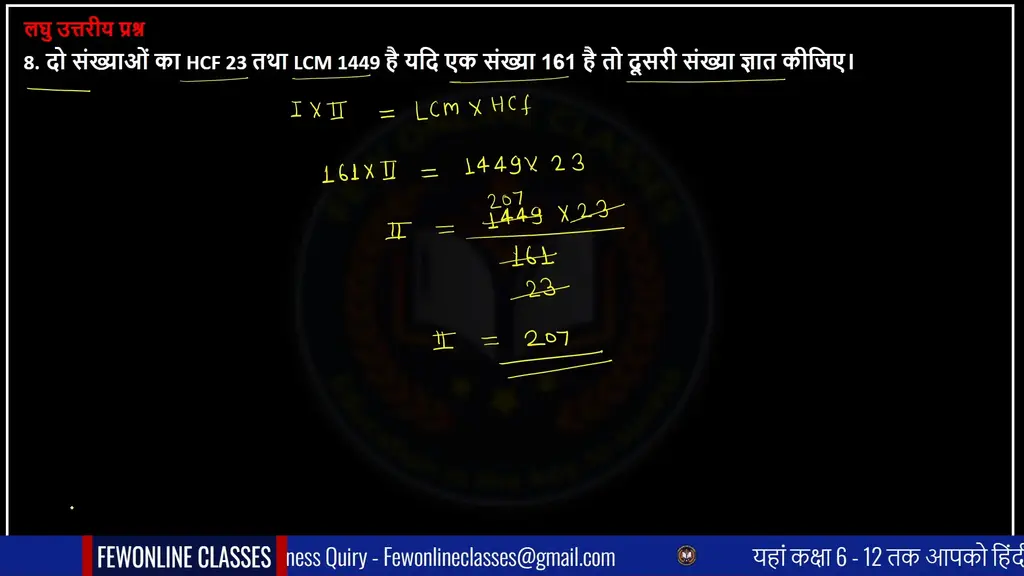
8. दो संख्याओं का एचसीएफ HCF 23 तथा एलसीएम LCM 1449 है यदि एक संख्या 161 है तो दूसरी संख्या ज्ञात कीजिए।
Ans. आप इस प्रश्न में देखोगे की मासा 23 लासा 1449 तथा पहली संख्या 161 है और हमें दूसरी संख्या ज्ञात करनी है। इसके लिए हम सबसे पहले सूत्र लिखेंगे और उसे सूत्र में हम Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers मान रखेंगे
यहां पर आपको मासा, लासा तथा पहली संख्या का मान class 10th maths chapter 1 exercise 1.2 solutions दिया हुआ है
ल0स0 × म0स0 = पहली संख्या × दूसरी संख्या
1449 × 23 = 161 × दूसरी संख्या
यहां पर आप देखोगे की 1449 की गुणा 23 से करवाने के बाद 161 से भाग देंगे तो हमारा आंसर 207 आ जाएगा।
9. सिद्ध कीजिए कि √3 एक अपरिमेय संख्या है।
Ans. माना √3 एक परिमेय संख्या है जहां P और q सहअभाज्य संख्याएं हैं। class 10 maths chapter 1 exercise 1.2 solutions
p/q = √3
क्रॉस गुणा करने पर
p = √3 q
दोनों पक्षों का वर्ग करने पर
(p)² = (√3q)²
p² = 3q² …………….(i)
p², 3 से विभाजित है अतः 3, p को भाग करेगा |……….(ii)
p = 3z जहां z पूर्णांक संख्या है।
p का मान समीकरण (i) में रखने पर
(3z)² = 3q²
9z² = 3q²
3 से 9 को भाग देने पर
3z² = q²
q², 3 से विभाजित है अतः 3, q को भाग करेगा |……..(iii)
समीकरण (ii) या (iii) से
3, p व q दोनों को भाग करता है जबकि हमने माना था, की p व q सह अभाज्य संख्याएं हैं।
परंतु इस तथ्य का विरोधाभास प्राप्त होता है अतः √3 एक अपरिमेय संख्या है।

10. संख्या 20570 का अभाज्य गुणनखंड ज्ञात कीजिए।
Ans. संख्या 20570 का अभाज्य गुणनखंड करने के लिए सर्वप्रथम संख्या को लिखेंगे और इसे जो है डिवाइड करेंगे तब इसके अभाज्य गुणनखंड कुछ class 10 maths ch 1 ex 1.2 solutions इस प्रकार होंगे
20570 = 2×5×11×11×17
20570 अभाज्य गुणनखंड = 2×5×11×11×17

11. नीचे दी गई आकृति में x, y तथा z के मान ज्ञात कीजिए।
Ans. हम नीचे दी गई संख्याओं के मान Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers कुछ इस प्रकार जो है ज्ञात करेंगे जैसा कि आपको इमेज class 10 ex 1.2 के माध्यम से समझाया गया है

12. सिद्ध कीजिए कि 2 – √3 एक अपरिमेय संख्या है।
Ans. माना 2 – √3 एक परिमेय संख्या है जहां पर हमें ज्ञात है कि 2 एक परिमेय संख्या है और दो परिमेय संख्याओं का अंतर परिमेय संख्या ही होता है। class 10th maths ex 1.2
(2 – √3- 2)
– √3
अर्थात √3 परिमेय संख्याहै।
जो की एक विरोधाभास प्राप्त होता है क्योंकि √3 एक अपरिमेय संख्या है अतः 2-√3 एक अपरिमेय संख्या होगी।

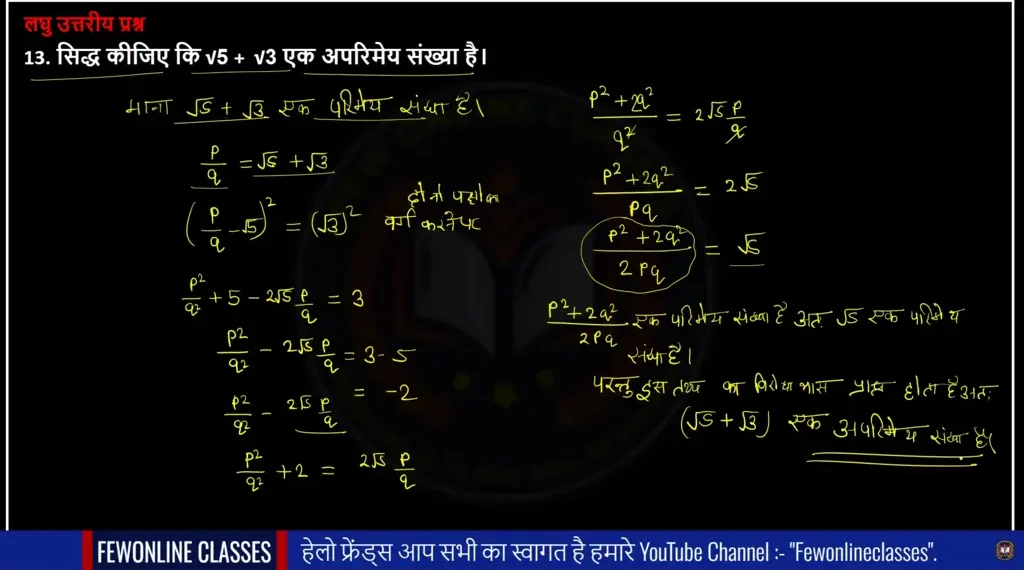
13. सिद्ध कीजिए कि √5 + √3 एक अपरिमेय संख्या है।
Ans. माना √5+√3 एक परिमेय संख्या है ।
इस सवाल को नीचे दिए class 10 math ex 1.2 गए इमेज के माध्यम से हम बहुत ही आसान तरीके से हल Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers करेंगे अगर आपको यह सवाल समझ में नहीं आता तो आपको इसका वीडियो का लिंक डिस्क्रिप्शन बॉक्स में दे दिया जाएगा
जहां से आप बहुत ही आसान श्री बालाजी प्रकाशन गणित अध्याय 1 वास्तविक संख्याएं अभ्यास प्रश्न 1.2 तरीके से वीडियो को देखकर इस अध्याय के समस्त प्रश्नों को हल Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers कर पाओगे।
class 10 math chapter 1 ex 1.2
दीर्घ उत्तरीय प्रश्न
Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers
14. सिद्ध कीजिए कि निम्न संख्याएं अपरिमेय है-
(i) (3 + √2)
(ii) (5 + 3√2)
(iii) 5√2
(iv) (4 – √3)
(v) (2 – √5)
(i) सिद्ध कीजिए कि (3 + √2) संख्याएं अपरिमेय है
Ans. माना 3+√2 एक परिमेय संख्या है जहां पर हमें ज्ञात है कि 3 एक परिमेय संख्या है और दो परिमेय संख्याओं का अंतर परिमेय संख्या ही होता है। class 10th maths chapter 1.2
(3 + √2- 3)
√2
अर्थात √2 परिमेय संख्याहै।
जो की एक विरोधाभास प्राप्त होता है क्योंकि √2 एक अपरिमेय संख्या है अतः 3+√2 एक अपरिमेय संख्या होगी।

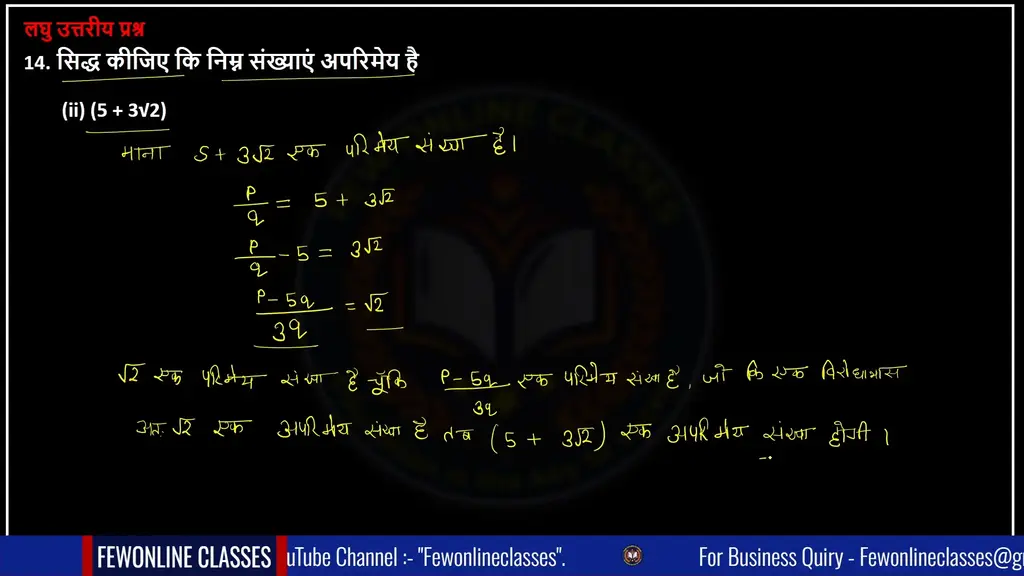
(ii) सिद्ध कीजिए कि 5 + 3√2 संख्याएं अपरिमेय है | class 10 maths chapter 1.2
Ans. माना 5+3√2 एक परिमेय संख्या है जहां P और q सहअभाज्य संख्याएं हैं।
p/q = 5 + 3√2
p/q – 5 = 3√2
p-5q /q = 3√2
p-5q /3q = √2
√2 एक परिमेय संख्या है चूंकि कि p-5q /3q एक परिमेय संख्या है जो की एक विरोधाभास है अतः √2 एक अपरिमेय संख्या है तब 5+3√2 एक अपरिमेय संख्या होगी।
(iii) सिद्ध कीजिए कि 5√2 संख्याएं अपरिमेय है | class 10 maths 1.2
Ans. माना 5√2 एक परिमेय संख्या है जहां P और q सहअभाज्य संख्याएं हैं।
p/q = 5√2
p/5q = √2
√2 एक परिमेय संख्या है चूंकि कि p/5q एक परिमेय संख्या है जो की एक विरोधाभास है अतः √2 एक अपरिमेय संख्या है तब 5√2 एक अपरिमेय संख्या होगी।

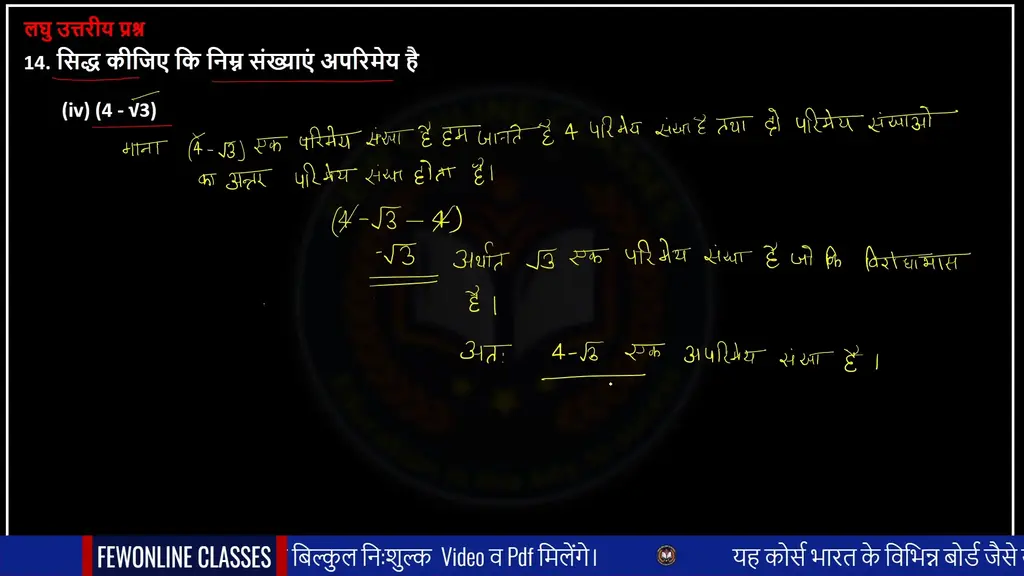
(iv) सिद्ध कीजिए कि 4 – √3 संख्याएं अपरिमेय है |
Ans. माना 4 – √3 एक परिमेय संख्या है जहां पर हमें ज्ञात है कि 4 एक परिमेय संख्या है और दो परिमेय संख्याओं का अंतर परिमेय संख्या ही होता है।
(4 – √3– 4)
– √3
अर्थात √3 परिमेय संख्याहै।
जो की एक विरोधाभास प्राप्त होता है क्योंकि √3 एक अपरिमेय संख्या है अतः 4 – √3 एक अपरिमेय संख्या होगी। ex 1.2 class 10
(v) सिद्ध कीजिए कि 2-√5 संख्याएं अपरिमेय है |
Ans. माना 2-√5 एक परिमेय संख्या है जहां पर हमें ज्ञात है कि 2 एक परिमेय संख्या है और दो परिमेय संख्याओं का अंतर परिमेय संख्या ही होता है।
(2-√5– 2)
– √5
अर्थात √5 परिमेय संख्याहै।
जो की एक विरोधाभास प्राप्त होता है क्योंकि √3 एक अपरिमेय संख्या है अतः 2-√5 एक अपरिमेय संख्या होगी। class 10 math ch 1 ex 1.2

class 10 math ch 1 ex 1.2
आपको इस Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers के समस्त सवालों को हल करवा कर दिखाया गया है अगर आपको फिर भी समस्या होती है तो आपको सबसे नीचे वीडियो का लिंक दिया गया है जहां पर आप बहुत ही आसान तरीके से इस अभ्यास के सवालों को सॉल्व class 10th maths chapter 1 ex 1.2 कर पाएंगे।
अगर श्री बालाजी प्रकाशन गणित अध्याय 1 वास्तविक संख्याएं अभ्यास प्रश्न 1.2 फिर भी कोई समस्या होती है तो आप हमें नीचे कमेंट बॉक्स में कमेंट कर class 10th maths ch 1 ex 1.2 सकते है और हम उसका जवाब वीडियो के माध्यम से इसी पोस्ट में Class 10 Maths Ch 1 Ex 1.2 Solutions Real Numbers अवश्य लिखेंगे।
class 10 math ch 1 ex 1.2 All Question in Balaji Publication
आपके यहां पर कक्षा 10 गणित अध्याय एक वास्तविक संख्याएं प्रश्नावली 1.1 के समस्त सवाल के हल यहां पर आपको मिलेंगे जिसे आप देखने के लिए इस नीचे दिए गए लिंक class 10 math ch 1 ex 1.2 पर क्लिक करके आप बहुत ही आसान तरीके से देख पाओगे।
class 10th maths chapter 1 exercise 1.1
श्री बालाजी प्रकाशन गणित कक्षा 10
आप यहां पर बालाजी प्रकाशन कक्षा 10 गणित का समस्त अध्याय मैं सम्मिलित अभ्यास प्रश्न बहुविकल्पीय प्रश्न विविध प्रश्नावली एनसीईआरटी अभ्यास प्रश्न स्वम मूल्यांकन परीक्षण के समस्त प्रश्न कोहल कर पाएंगे और उनके अध्याय क्रम से मिल जाएंगे
अध्याय 1 वास्तविक संख्याएं
अभ्यास प्रश्न 1.1
अभ्यास प्रश्न 1.2
विविध प्रश्नावली
बहुविकल्पीय प्रश्न
स्वमूल्यांकन परीक्षण
एनसीईआरटी अभ्यास प्रश्न

